2022/8/10 / 最終更新日時 : 2022/9/22 オアシス塾長 lesson

3次方程式の因数分解(a^3+b^3+c^3-3abc)に関して

a^3 + b^3 = (a+b)(a^2 – ab + b^2)

数学1Aの数と式に関して、基礎的な公式の中で最も複雑なものは

$a^3 \pm b^3 = (a \pm b)(a^2 \mp ab + b^2)$

この辺りかなと個人的には思っています。曖昧に覚えてしまっている方は正確に覚えることができるまで常に検算を行っておきましょう。

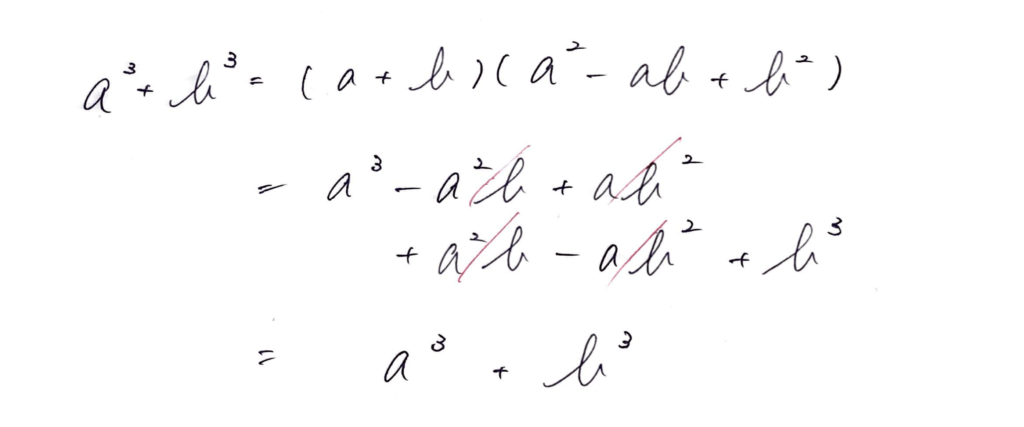
a^3 + b^3 = (a+b)(a^2 - ab + b^2)

a^3 – b^3 = (a-b)(a^2 + ab + b^2)

マイナスになった時も同様に検算ができますが、どの箇所のプラスとマイナスが変化しているかに注意しましょう。

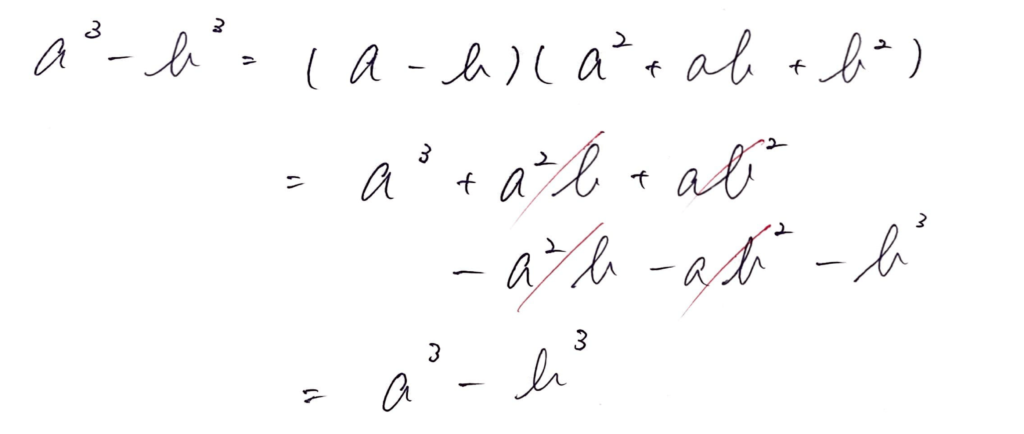
a^3 - b^3 = (a-b)(a^2 + ab + b^2)

a^3 + b^3 + c^3 – 3abc

さて本題は

$a^3+b^3+c^3$

に関してです。こちらが出た時に、どうすればいいかわからないということをよく聞きます。

正直こちらの問題は、ある特殊な因数分解を覚えておければすぐに解けるのですが、必須で暗記というわけでもないので、論点に上がることがあります。

結論から言いましょう。

$a^3+b^3+c^3 - 3abc = (a+b+c)(a^2+b^2+c^2-ab-bc-ca)$

こう因数分解できるんですね。丸っと暗記ができるならokなのですが、それも難しいと思うので、導出をおすすめします。

実は↑で出た

$a^3 + b^3 = (a + b)(a^2 - ab + b^2)$

これの、bにb+cに代入すると、導出できます。置いておきますね。

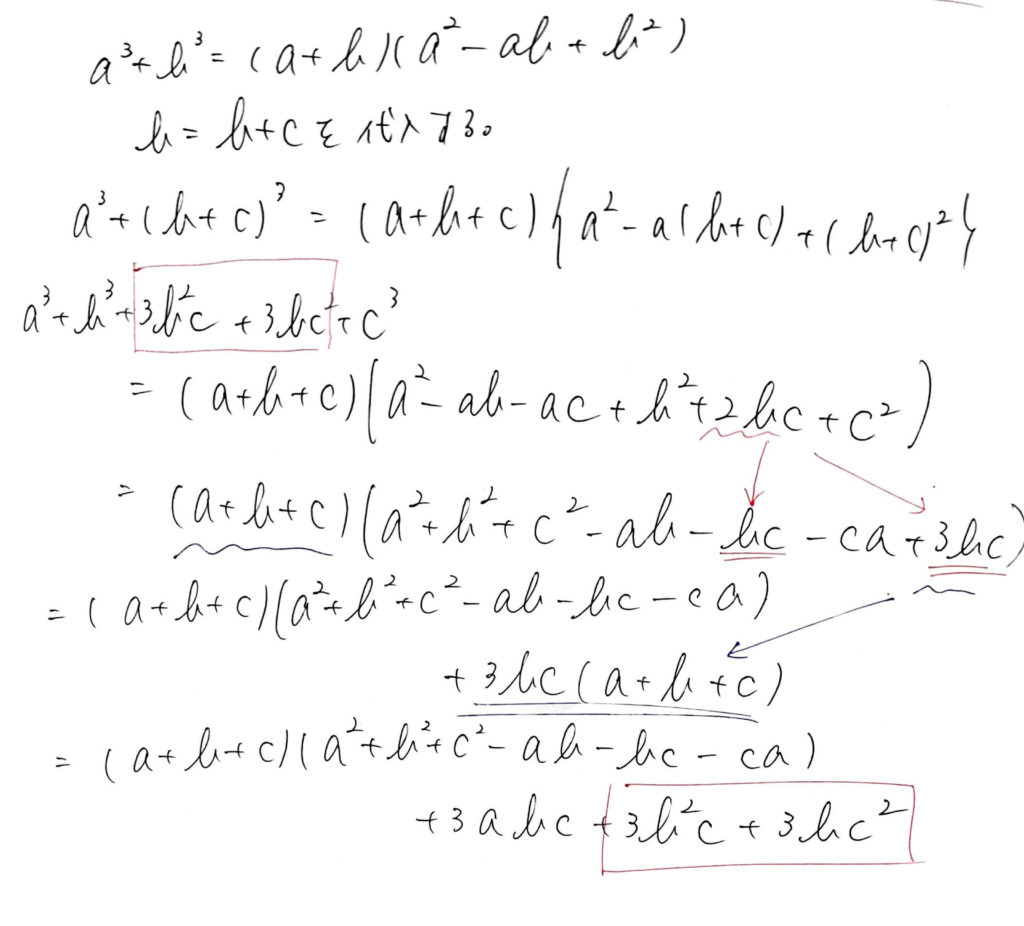
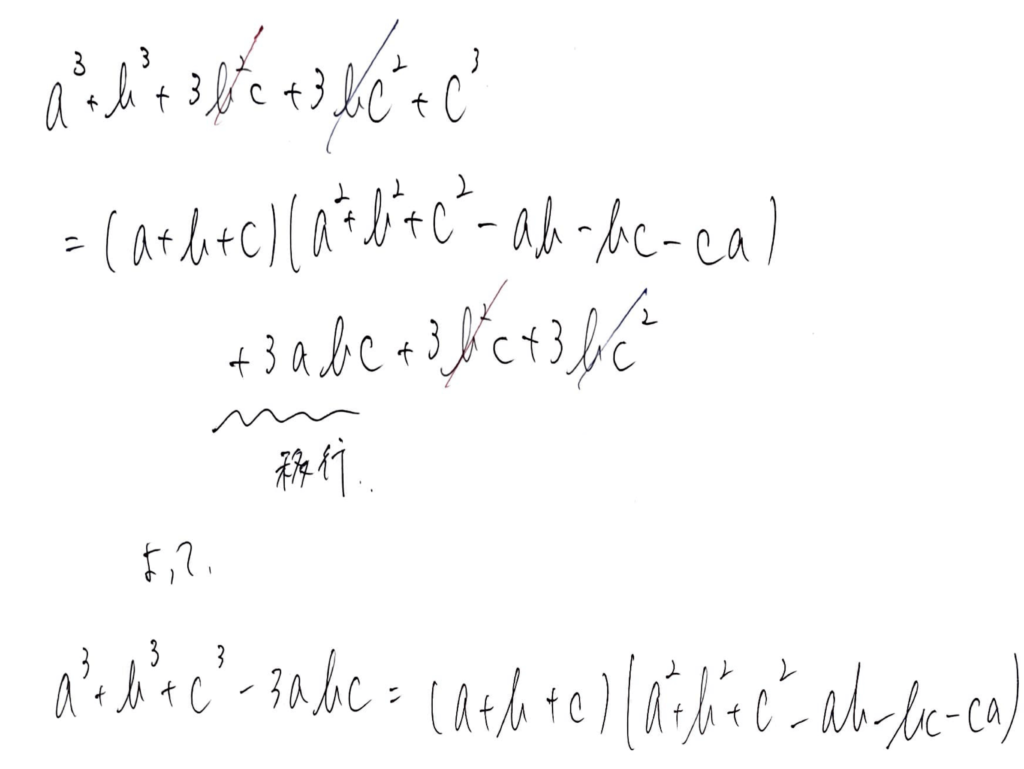
a^3+b^3+c^3 - 3abc = (a+b+c)(a^2+b^2+c^2-ab-bc-ca)

a^3+b^3+c^3 - 3abc = (a+b+c)(a^2+b^2+c^2-ab-bc-ca)

というわけで、出てきました。

学校によっては問題の中で誘導がありますが、先にここまでわかっていると、計算間違いも減りますし、解くスピードも上がります。

a^3 ± 3a^2b + 3ab^3 ± b^3 = (a±b)^3

質問が多かったようなので、念の為

$(a+b)^3, (a-b)^3$

のお話を追加しておきます。

まずは展開の公式、

$(a+b)^3 = a^3 + 3a^2b + 3ab^3 + b^3$
$(a-b)^3 = a^3 - 3a^2b + 3ab^3 - b^3$

こちらを実施しましょう。暗記をしなくても、一度

$(a+b)^3$
$= ( a + b )^2 * (a+b)$
$= ( a^2 + 2ab + b^2) * (a+b)$
$= a^3 + 3a^2b + 3ab^3 + b^3$

といった形で、2乗を先に実施して展開をすることでも計算が可能です。

あとは逆に辿れば

$a^3 + 3a^2b + 3ab^3 + b^3 = (a+b)^3$
$a^3 - 3a^2b + 3ab^3 - b^3 = (a-b)^3$

このように因数分解ができますね。

引き続きこちらでは受験に必要な情報を発信していきます。ご質問はhttps://twitter.com/edutechwork まで。

それでは。

カテゴリー: lesson

“3次方程式の因数分解(a^3+b^3+c^3-3abc)に関して” に対して3件のコメントがあります。

コメントを残す

前の記事

受験に必要な考え方：成功への道筋を示す

2022/8/1

次の記事

苦手意識について

2022/8/13